【ベストコレクション】 y=x reflection 283540-Y x reflection rules 6

Reflecting shapes diagonal line of reflection Our mission is to provide a free, worldclass education to anyone, anywhere Khan Academy is a 501(c)(3) nonprofit organizationLearn termreflection rotation = (x,y)=( x, y) with free interactive flashcards Choose from 500 different sets of termreflection rotation = (x,y)=( x, y) flashcards on QuizletGraph functions using reflections about the xaxis and the yaxis Another transformation that can be applied to a function is a reflection over the x – or y axis A vertical reflection reflects a graph vertically across the x axis, while a horizontal reflection reflects a graph horizontally across the y

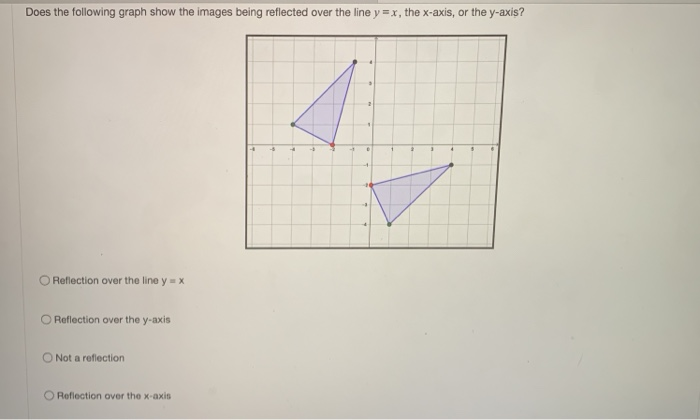
Solved Does The Following Graph Show The Images Being Chegg Com

Y x reflection rules 6

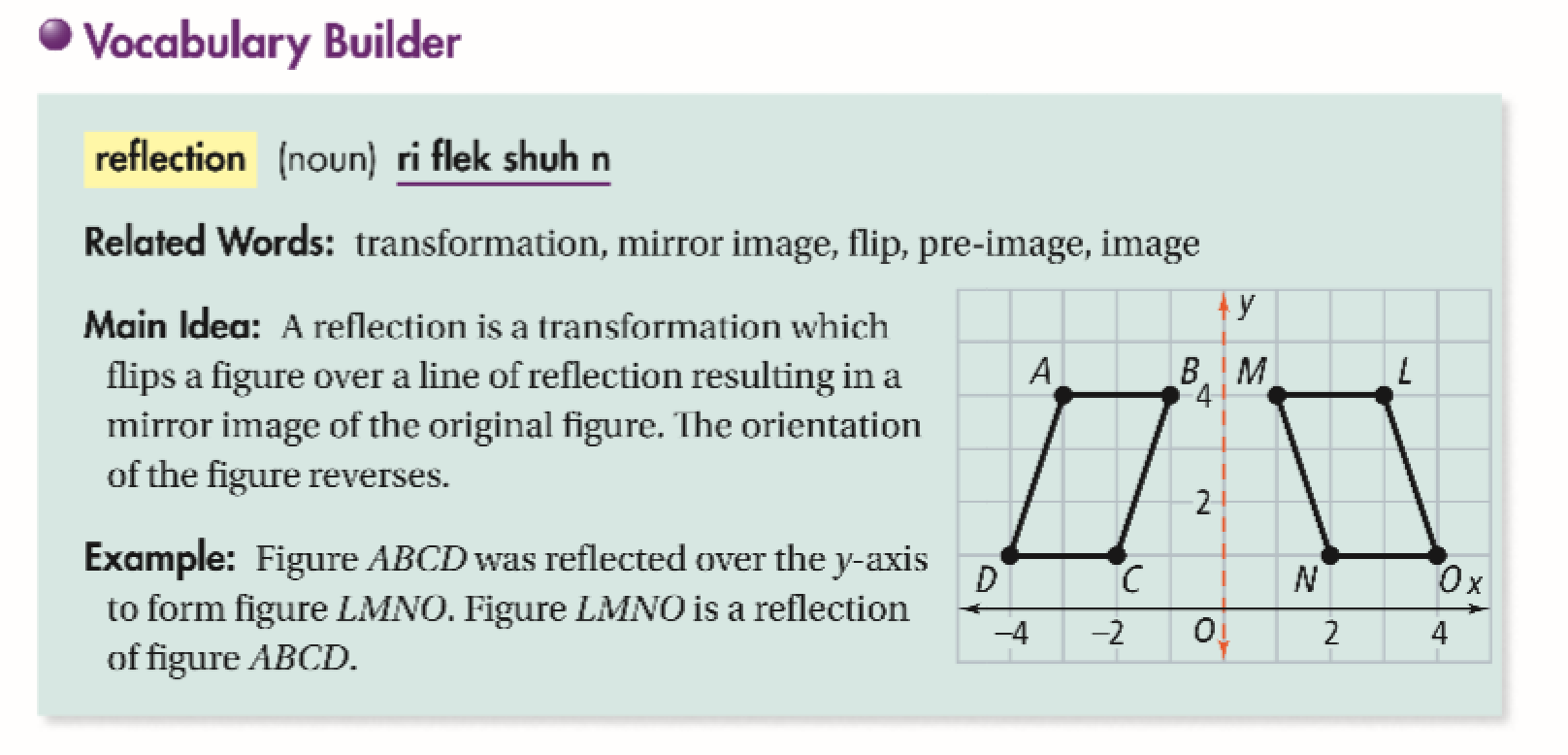
Y x reflection rules 6-Get the free "Reflection Calculator MyALevelMathsTutor" widget for your website, blog, Wordpress, Blogger, or iGoogle Find more Education widgets in WolframAlphaReflections A reflection is a transformation representing a flip of a figure Figures may be reflected in a point, a line, or a plane When reflecting a figure in a line or in a point, the image is congruent to the preimage A reflection maps every point of a figure to an image across a fixed line The fixed line is called the line of reflection

Common Reflections Key Stage 3

A reflection of the point across the xaxis a reflection of the point across the yaxis a reflection of the point across the line y =Tutorial on transformation matrices in the case of a reflection on the line y=xYOUTUBE CHANNEL at https//wwwyoutubecom/ExamSolutionsEXAMSOLUTIONS WEBSITY = f (x) y = f (−x) Remember, the only step we have to do before plotting the f (x) reflection is simply divide the xcoordinates of easytodetermine points on our graph above by (1) When we say "easytodetermine points" what this refers to is just points for which you know the x

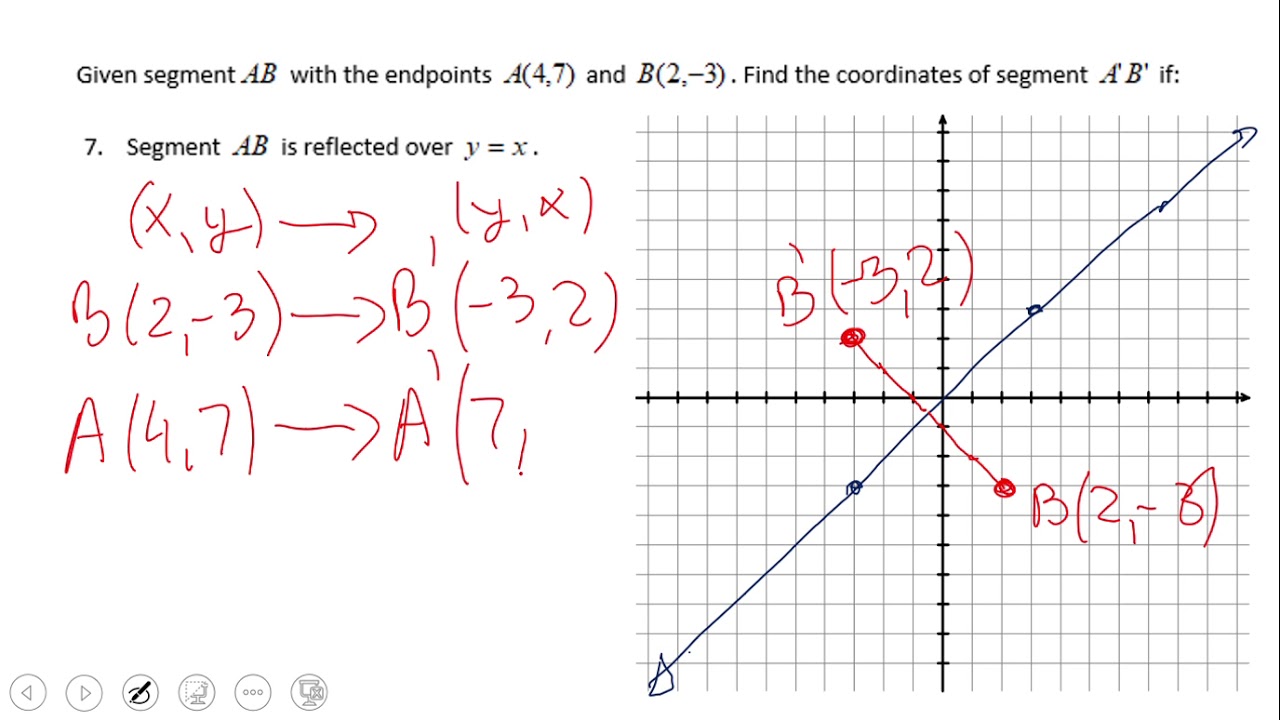
The reflection transformation may be in reference to the coordinate system (X and Yaxis) Reflections in the Coordinate Plane The reflection transformation may be in reference to X and Yaxis Reflection over Xaxis When a point is reflected across the Xaxis, the xcoordinates remain the same But the Ycoordinates are transformed into itsReflection about the line y=x Once students understand the rules which they have to apply for reflection transformation, they can easily make reflection transformation of a figure For example, if we are going to make reflection transformation of the point (2,3) about xaxis, after transformation, the point would be (2,3)Geometry reflection A reflection is a "flip" of an object over a line Let's look at two very common reflections a horizontal reflection and a vertical reflection

Reflection about the line y = x Once students understand the rules which they have to apply for reflection transformation, they can easily make reflection transformation of a figure Let us consider the following example to have better understanding of reflectionTransitive property If 8 equals x and x equals y, then 8 equals yThe transformation from the first equation to the second one can be found by finding a a, h h, and k k for each equation y = a√x− hk y = a x h k Factor a 1 1 out of the absolute value to make the coefficient of x x equal to 1 1 y = √x y = x Find a a, h h, and k k for y = √x y = x a = 1 a = 1

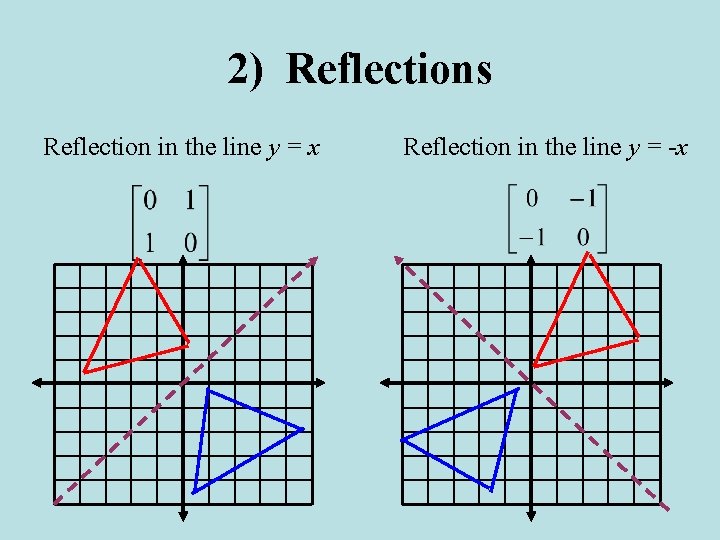
4 4 Transformations With Matrices 2 Reflections And

Solved Does The Following Graph Show The Images Being Chegg Com

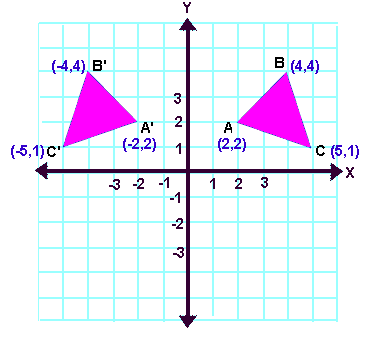
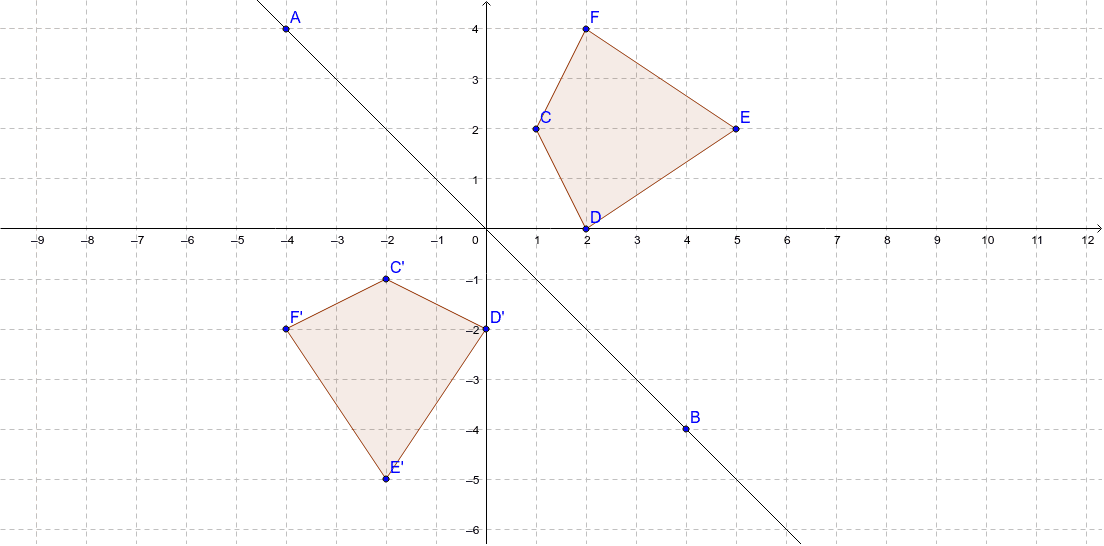
 We can differentiate 2D and 3D reflection by adding Zaxis The Zaxis shows the depth of the surface In the Reflection process, the size of the object does not change We can represent Reflection by using the following three waysReflection along with xy Plane In the xy plane reflection, the value of z is negative x 1 = x 0 y 1 = y 0Reflections across the line y = x A reflection across the line y = x switches the x and ycoordinates of all the points in a figure such that (x, y) becomes (y, x) Triangle ABC is reflected across the line y = x to form triangle DEF Triangle ABC If we reflect $(x,y)$ about $y=x$ then we get $(y,x)$ And because $x^2y^2=y^2x^2$ this can also be represented by a rotation Using this we get

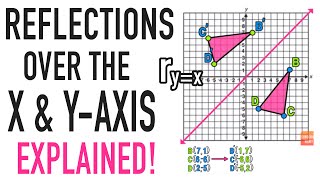
Reflections Over The X Axis And Y Axis Explained Youtube

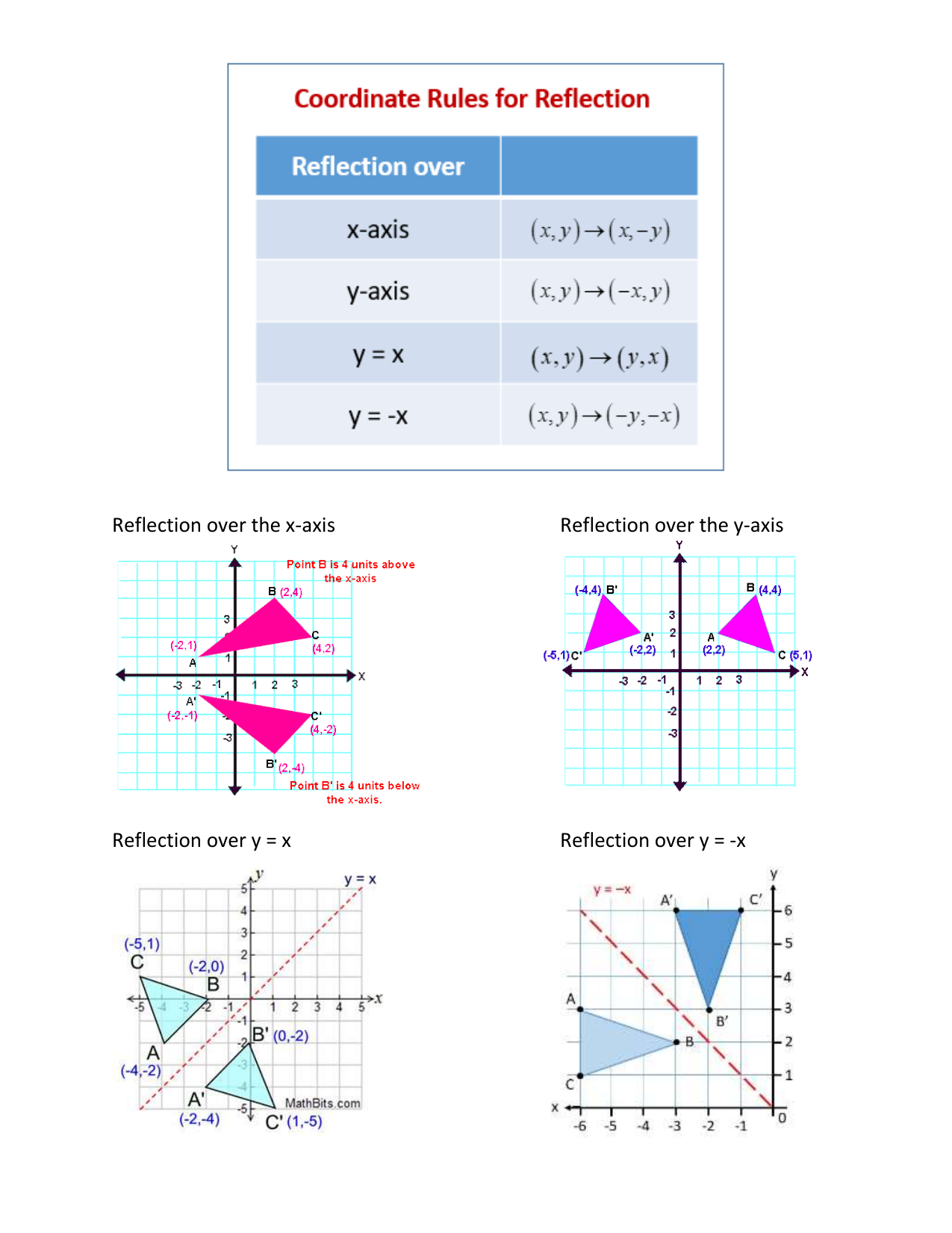
Reflection Rules Toolkit

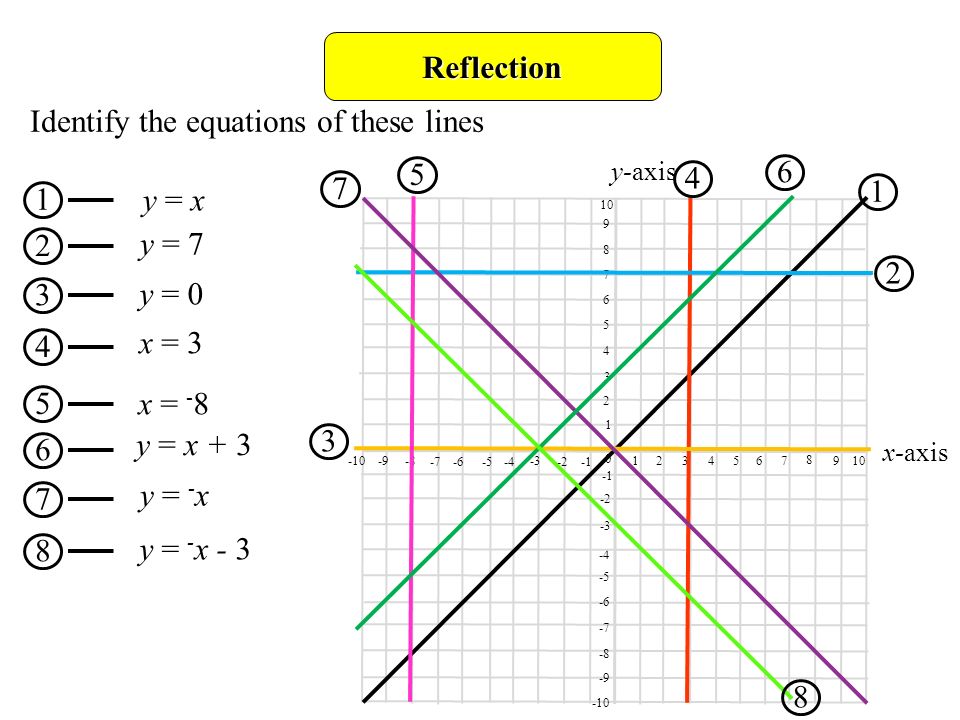
 The most common lines of reflection are the xaxis, the yaxis, or the lines y = x or y = −x Notice that the notation tells you exactly how each (x,y) point changes as a result of the transformation Write the notation that represents the reflection of the preimage to the image in the diagram below What are the 4 reflection rules?2D Geometrical Transformations Assumption Objects consist of points and lines A point is represented by its Cartesian coordinates P = (x, y)Geometrical Transformation Let (A, B) be a straight line segment between the points A and BTherefore, X, Y is the reflection of point and is changed as X, Y in the region of YAxis A Condition of Reflection when Y = X Take the case where a point is reflecting across a line Y=X Now, the X and Y coordinates will interchange their positions However, the signs get negated/cancelled when the point of reflection takes place over

A Translation X Y X 5 Y Reflection Across Y Axis B Translation X Y X Y 5 Brainly Com

Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines

This is a KS3 lesson on reflecting a shape in the line y = x using Cartesian coordinates It is for students from Year 7 who are preparing for GCSE This page includes a lesson covering 'how to reflect a shape in the line y = x using Cartesian coordinates' as well as a 15question worksheet, which is printable, editable and sendableY = x 2 1 Reflection in the xaxis Solution y = x 2 1 → y = x 2 1 y = x 2 1 Graph Close Example Point P moves on the xaxis Minimum value of AP PB = ?Again, Fig 1 is y = f(x) Its reflection about the xaxis is y = −f(x) Every yvalue is the negative of the original f(x) Fig 3 is the reflection of Fig 1 about the yaxis Every point that was to the right of the origin gets reflected to the left And every point that was on

A Line Segment Goes From 1 2 To 4 1 The Line Segment Is Reflected Across X 1 Reflected Across Y 3 And Then Dilated About 2 2 By A Factor

Reflecting A Shape In Y X Using Cartesian Coordinates Key Stage 3

Reflections across y=x Click and drag the blue dot and watch it's reflection across the line y=x (the green dot) Pay attention to the coordinatesReflection over the line $$ y = x $$ A reflection in the line y = x can be seen in the picture below in which A is reflected to its image A' The general rule for a reflection in the $$ y = x $$ $ (A,B) \rightarrow (\red B, \red A ) $ Diagram 6 Applet You can drag the point anywhere you wantFunctions of graphs can be transformed to show shifts and reflections Graphic designers and 3D modellers use transformations of graphs to design objects and images

Reflection Over The Y X Line Youtube

Reflection Transformation

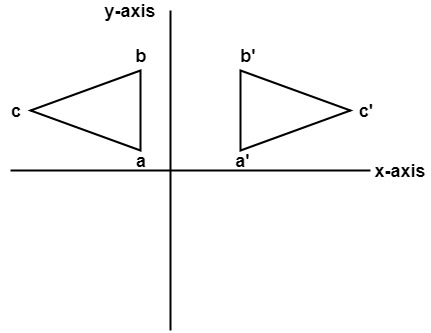
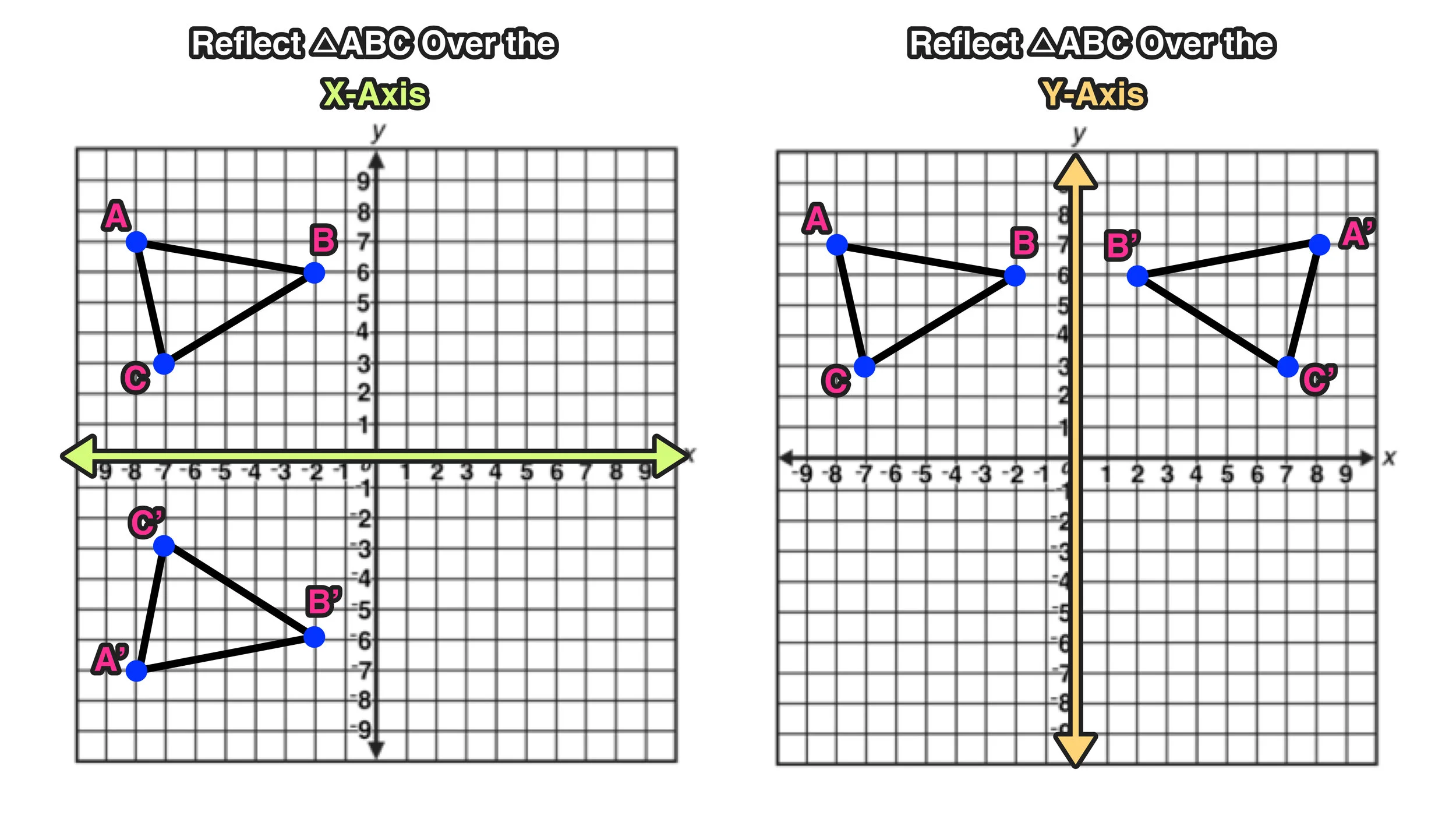
A math reflection flips a graph over the yaxis, and is of the form y = f (x) Other important transformations include vertical shifts, horizontal shifts and horizontal compression Let's talk about reflections Now recall how to reflect the graph y=f of x across the x axisThe reflection of the point (x,y) across the yaxis is the point (x,y) bullet Reflect over the y = xrefX3 When you reflect a point across the line y = x, the xcoordinate and ycoordinate change places If you reflect over the line y = x, the xcoordinate and ycoordinate change places and are negated (the signs are changed) The reflection Reflection across the yaxis changes the sign of the x coordinate only, that is, (x, y) becomes (x, y) What algebraic property is 8 equals x and x equals y?

Reflection Mathbitsnotebook A1 Ccss Math

Reflection

18 B 6 A point has the coordinates (0, k) Which reflection of the point will produce an image at the same coordinates, (0, k)?Reflecting functions examples We can reflect the graph of any function f about the xaxis by graphing y=f (x) and we can reflect it about the yaxis by graphing y=f (x) We can even reflect it about both axes by graphing y=f (x) See how this is applied to solve various problems This is the currently selected itemWe can also reflect the graph of a function over the xaxis (y = 0), the yaxis(x = 0), or the line y = x Making the output negative reflects the graph over the x axis, or the line y = 0 Here are the graphs of y = f ( x ) and y = f ( x )

Reflection Mathbitsnotebook A1 Ccss Math

Point 4 3 Is Reflected Over The Line Y X What Are The Coordinates Of The Reflection Mathskey Com

Reflection about line y=x The object may be reflected about line y = x with the help of following transformation matrix First of all, the object is rotated at 45° The direction of rotation is clockwise After it reflection is done concerning xaxis The last step is the rotation of y=x back to its original position that is counterclockwiseIn a reflection transformation, all the points of an object are reflected or flipped on a line called the axis of reflection or line of reflection Example A reflection is defined by the axis of symmetry or mirror lineIn the above diagram, the mirror line is x = 3∴ Image of the point P (x, y) under the reflection about the line y = x is the point P (y, x) Hence, if R denotes the reflection in the line y = x, then R P (x, y)→ P' (y, x) Reflection in the line y = x y = x is an equation of the line which makes an angle of 135° with the positive direction of X axis

Computer Graphics Reflection Javatpoint

Reflections And Symmetry Section 4 3 Reflection In

This is a KS3 lesson on reflecting a shape in the line y = −x using Cartesian coordinates It is for students from Year 7 who are preparing for GCSE This page includes a lesson covering 'how to reflect a shape in the line y = −x using Cartesian coordinates' as well as a 15question worksheet, which is printable, editable and sendable3 people liked this ShowMe Flag ShowMe Viewed after searching for reflection over the line y=x reflection over yaxis Reflection over y=x is over of equals percent over 100 reflect over x= 1 You must be logged into ShowMeRelated Pages Properties Of Reflection Transformation More Lessons On Geometry What is Reflection?

Reflection Over The X And Y Axis The Complete Guide Mashup Math

What Does It Mean To Reflect Over The Y X Line Quora

Reflection of a Point In these printable worksheets for grade 6 and grade 7 reflect the given point and graph the image across the axes and across x=a, y=b, where a and b are parameters Choose the Correct Reflection This practice set tasks 6th grade and 7th grade students to identify the reflection of the given point from the given optionsReflect over the xaxis When you reflect a point across the xaxis, the xcoordinate remains the same, but the ycoordinate is transformed into its opposite (its sign is changed) If you forget the rules for reflections when graphing, simply fold your paper along the xaxis (the line of reflection) to see where the new figure will be located Or you can measure how far your points are away I start with e^x which is a curve that follows y=0 then starts to rise more abruptly at x=0 If f (x) Makes you reflect over the x axis Then e^x will do a neccesary reflection for reflecting it about y = 2 Then I add 2 to the end of f (x) = (e^x)2 = 2e^x Although on my homework they say the correct answer is 4 e^x

Reflection Transformation

Reflection Rules How To W 25 Step By Step Examples

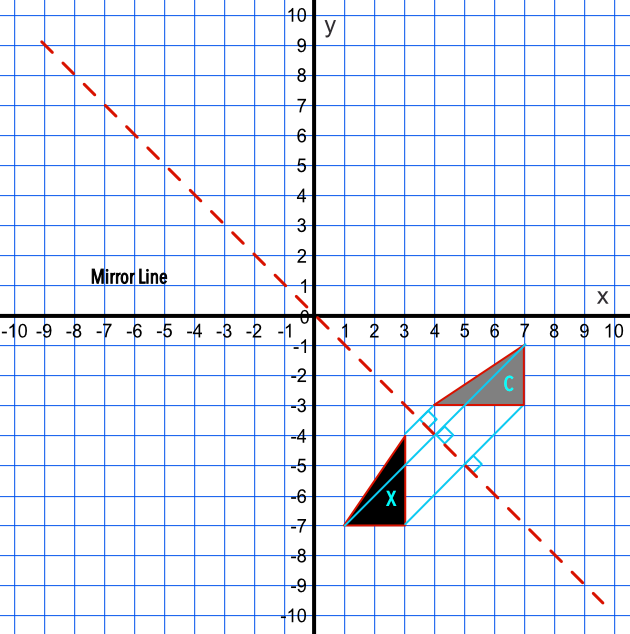
 Solved Examples – Reflection of Point using Graph Paper Q1 Write down the coordinates of the images of the points and when reflected in the axis Ans When a point is reflected in the axis, the coordinate remains the same while the y coordinate changes its sign under reflection in the axisA graph was reflected in the line y = x Its Cheggcom 7 A graph was reflected in the line y = x Its reflection image is shown Determine an equation of the original graph in terms of x and y Y 5 А у су B 41 DW4 4 y = Question 7 A graph was reflected in the line y = x Reflection Across Y=X Reflection Across Y=X How do you graph a reflection?

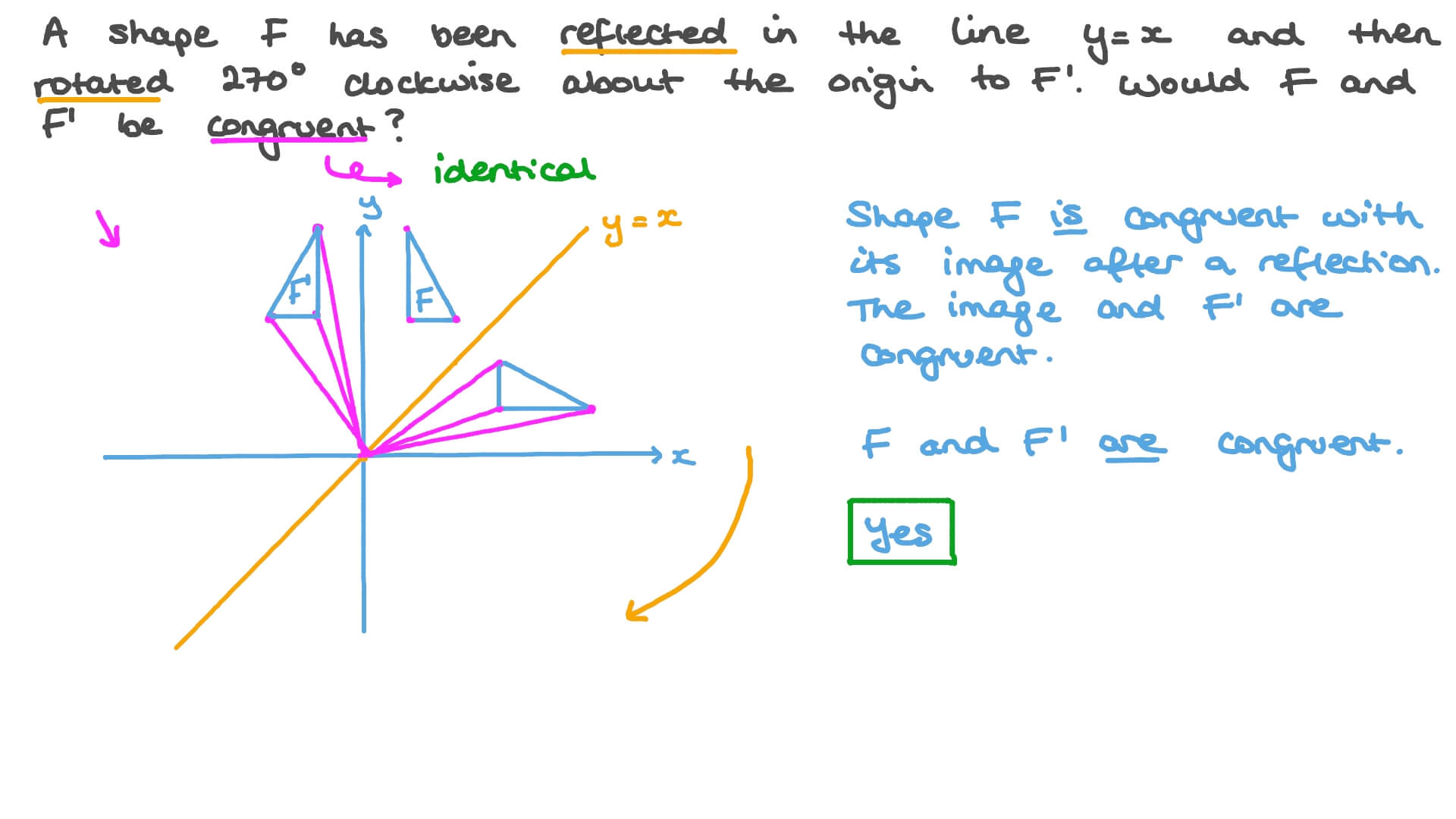
Question Video Understanding The Effects Of Reflection And Rotation On A Shape Nagwa

Math Alive Geometry 1

 👉 Learn how to reflect points and a figure over a line of symmetry Sometimes the line of symmetry will be a random line or it can be represented by the xHow To Given a function, reflect the graph both vertically and horizontally Multiply all outputs by –1 for a vertical reflection The new graph is a reflection of the original graph about the xaxis Multiply all inputs by –1 for a horizontal reflection

Transformation Reflection Over The Line Y X Youtube

Reflection Rules How To W 25 Step By Step Examples

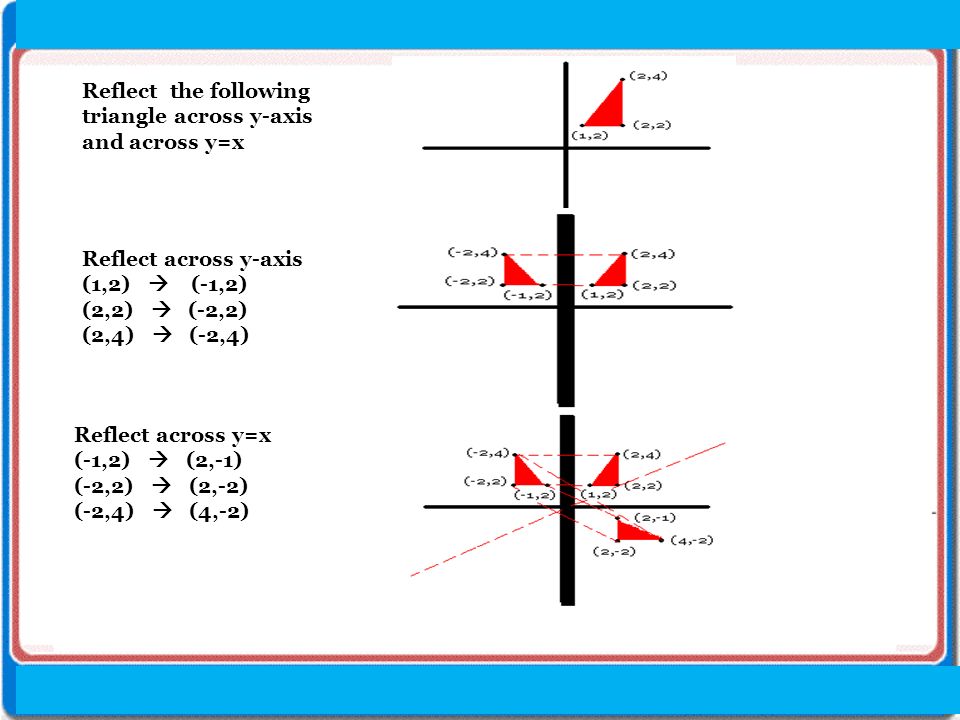
Reflections 30 Reflect Across Y X X Y Y X Reflect Across X Axis X Y X Y Reflect Across Y Axis X Y X Y Reflect Across Y X Reflect Across Ppt Download

Reflection Objectives D Grade Reflect Shapes In Lines

Reflection Over The Line Y X Geogebra

Reflections

1

How To Graph Reflections Across Axes The Origin And Line Y X Video Lesson Transcript Study Com

Lesson On Line Of Reflection Y X

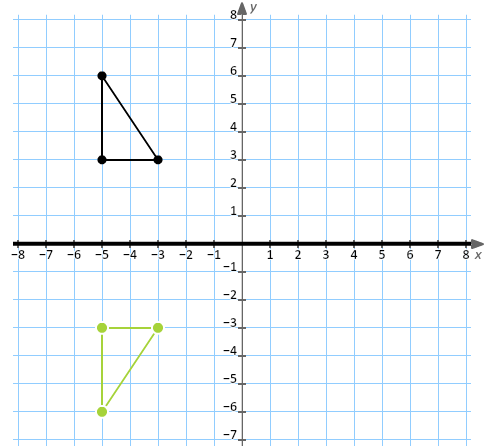
Reflection In A Cartesian Plane Lexique De Mathematique

Reflection Over The Line Y X Math Showme

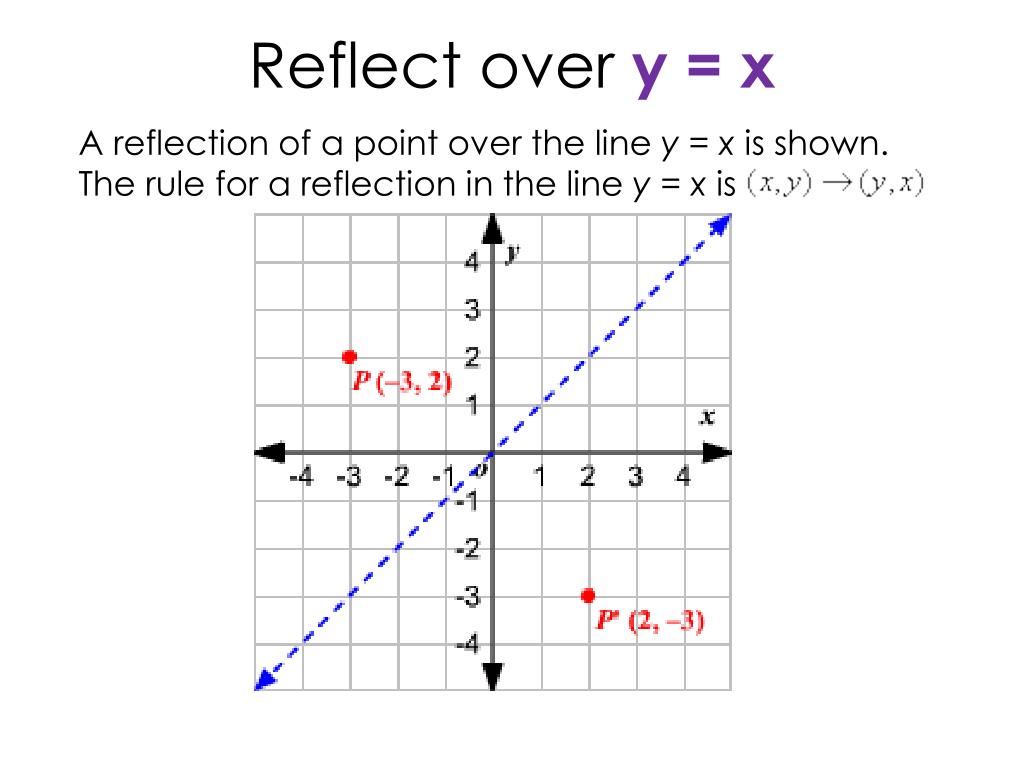
Ppt Reflect Over Y X Powerpoint Presentation Free Download Id

Reflections Ck 12 Foundation

Solution After A Reflection In The Line Y X 2 4 Is The Image Of Point N What Is The Original Location Of Point N

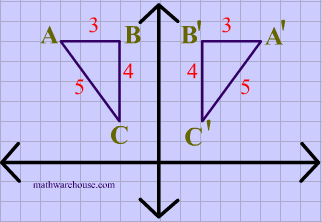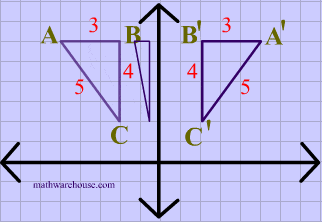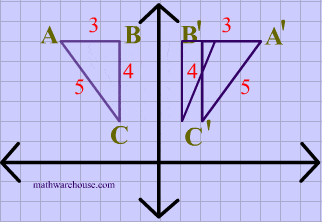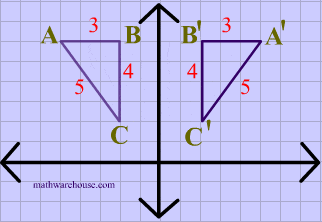
Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines

Reflections Math Analysis Functions

Reflection In Geometry Examples Solutions Videos Worksheets Games Activities

Computer Graphics Reflection Javatpoint

Ppt 9 3 Perform Reflections Powerpoint Presentation Free Download Id

Reflection Mathbitsnotebook A1 Ccss Math

Reflection Transformation Matrix

Translation With Geogebra Figure 2 Reflection Through Line Y X With Download Scientific Diagram

Reflecting Points Video Reflections Khan Academy

Biomath Transformation Of Graphs

S1 Work For Problem Ii About Reflection Respect To The Y X Line But Download Scientific Diagram

Transformations Of Graphs

Y X 2

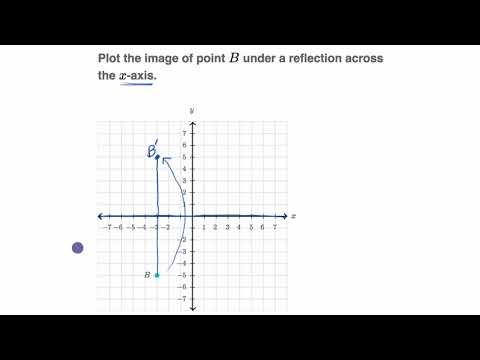
Reflecting Shapes Video Reflections Khan Academy

What Is A Line Of Reflection Printable Summary Virtual Nerd

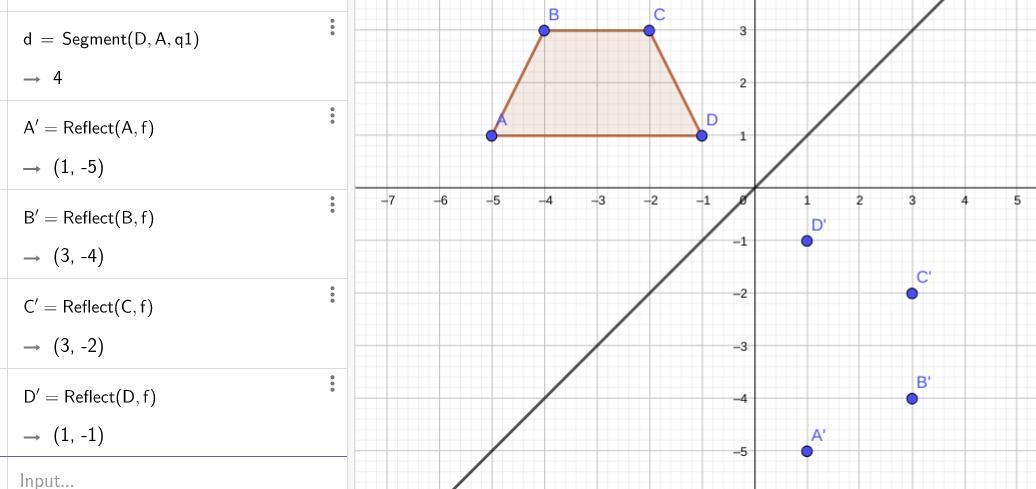
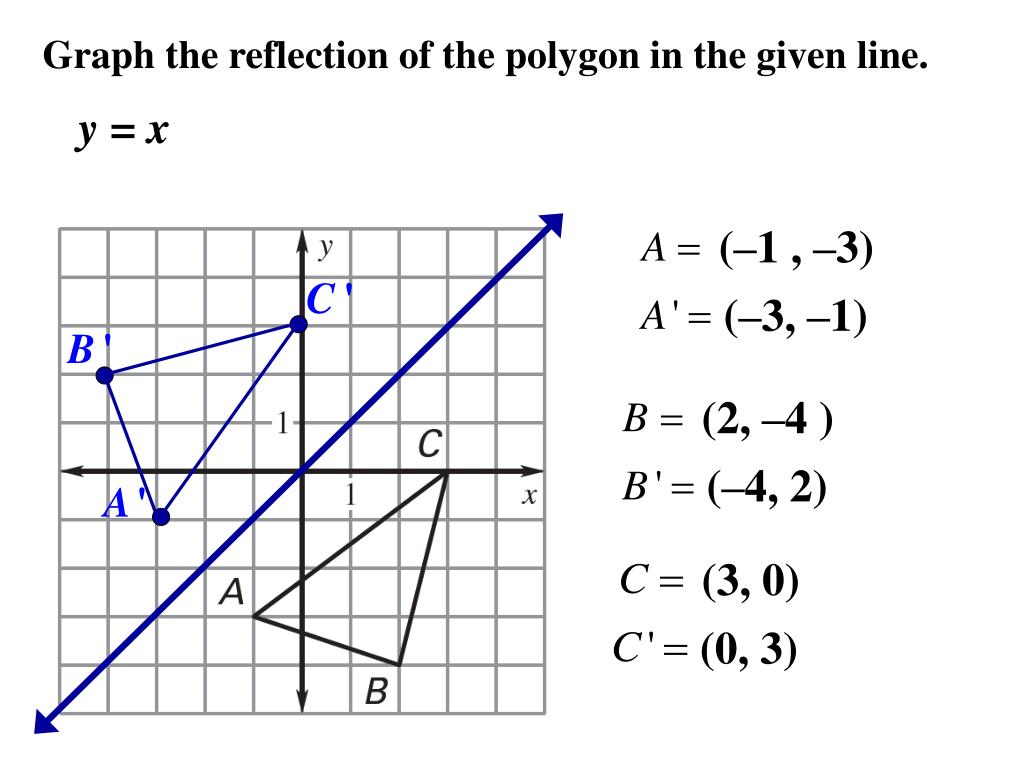
Trapezoid Abcd Is Reflected Over The Line Y X What Rule Shows The Input And Output Of The Reflection And What Is The New Coo

Reflections Geometry Abroad

1

Reflection Rules How To W 25 Step By Step Examples

Reflection In The Line Y X Transformation Matrix Youtube

Reflection Over Y X Math Geometry Showme

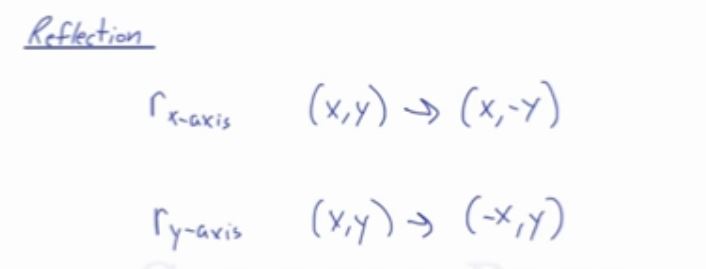
Learn About Reflection Over An Axis Over X Axis Or Y Axis

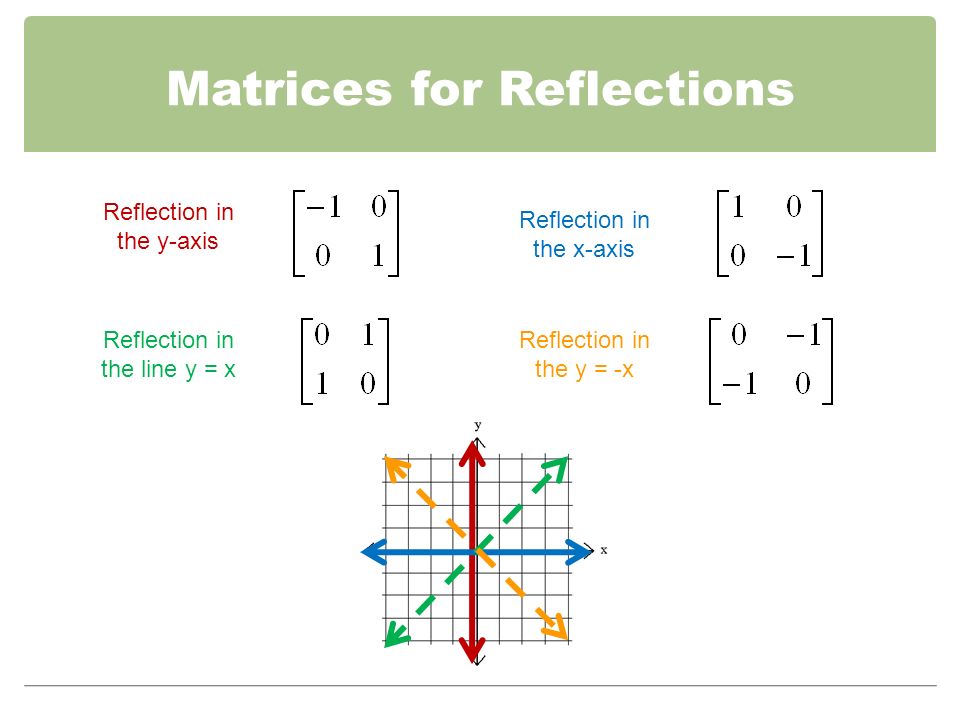
4 4 Geometric Transformations With Matrices Objectives To Represent Translations And Dilations W Matrices To Represent Reflections And Rotations With Ppt Download

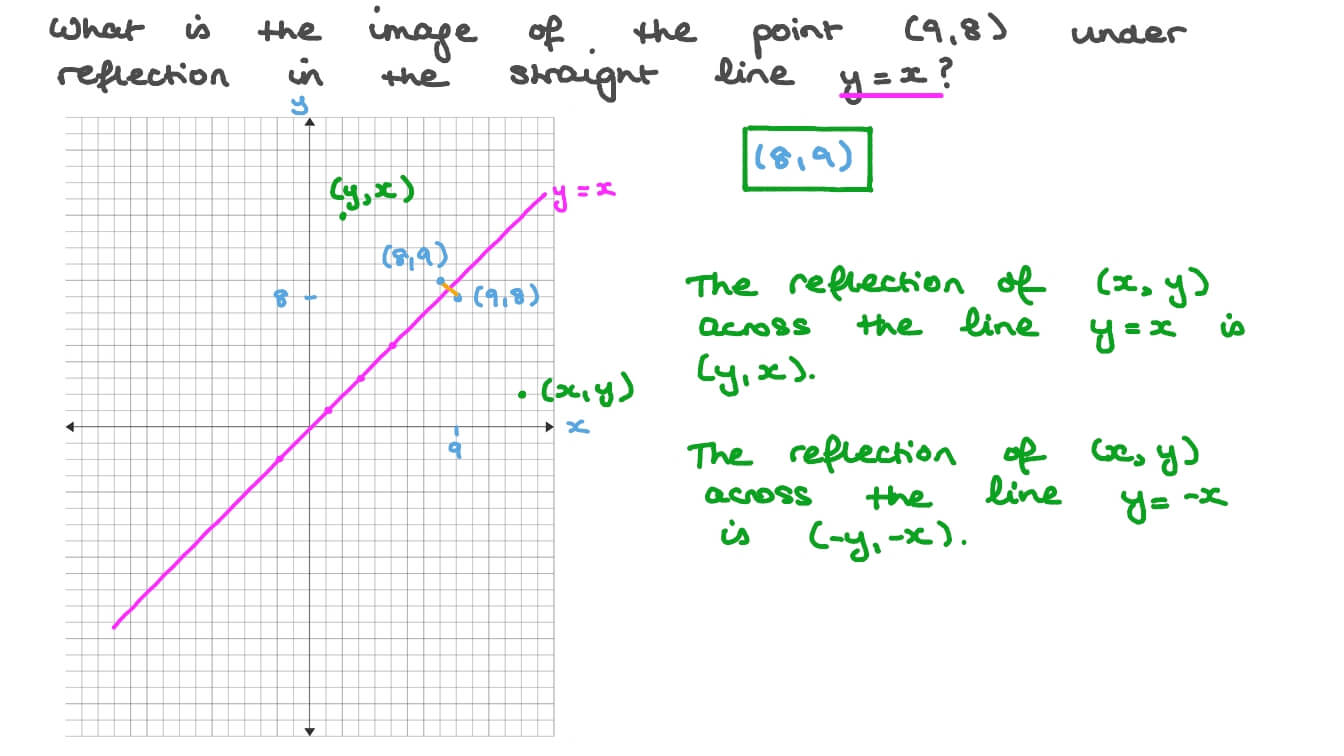
Question Video Determining The Position Of A Point After Reflecting In A Given Straight Line Given The Point S Coordinates Nagwa

Picture Of Reflection In The Line Y X Reflection Math Common Myths Types Of Reflection

Reflection

Picture Of Reflection Across Y Axis Reflection Math Math Reflection

Common Reflections Key Stage 3

How To Prove Say That Point X Y Becomes Y X On A Reflection On The Line Y X Using Only Geometry Quora

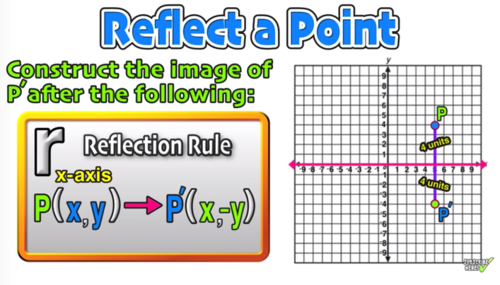
Reflection Over The X And Y Axis The Complete Guide Mashup Math

Compositions Of Reflections In Math Interactive Demonstration On How To Perform A Composition

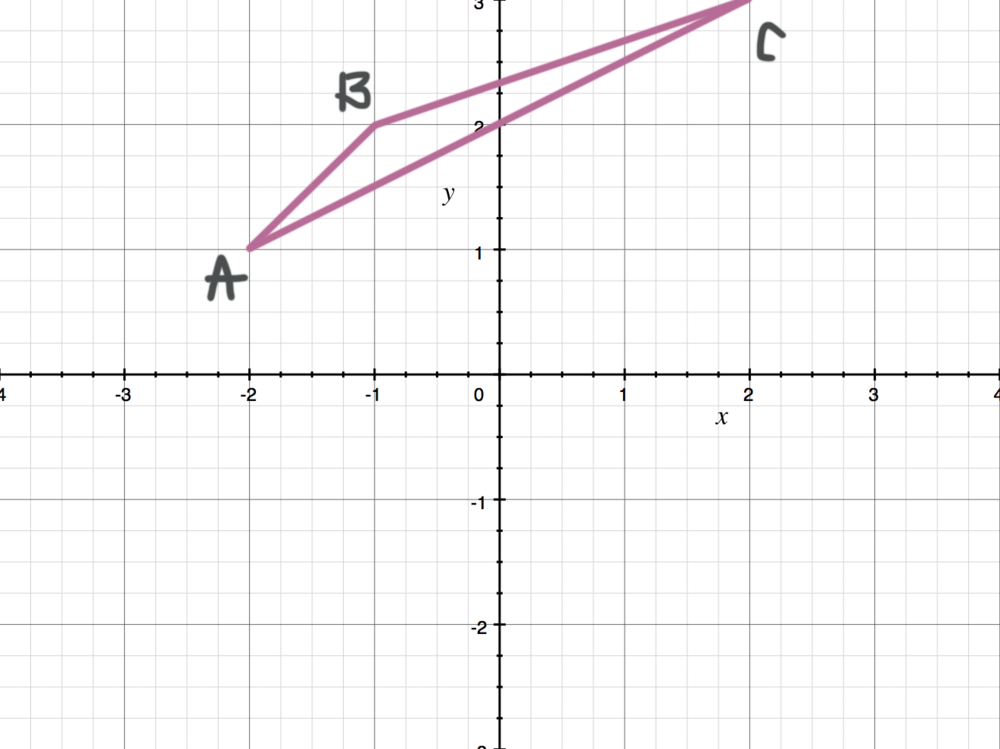
Reflecting Figures In Coordinate Space Krista King Math Online Math Tutor

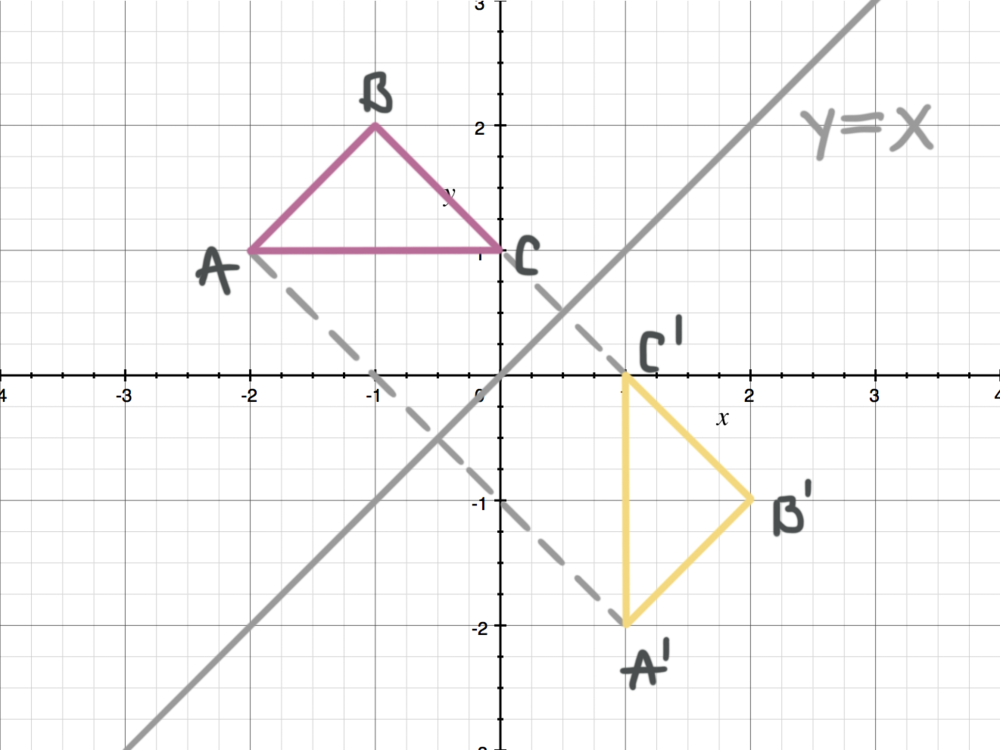
Reflecting Figures In Coordinate Space Krista King Math Online Math Tutor

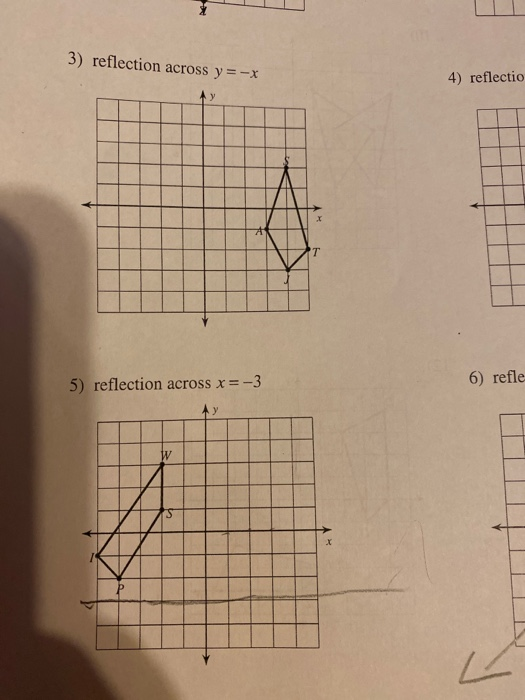
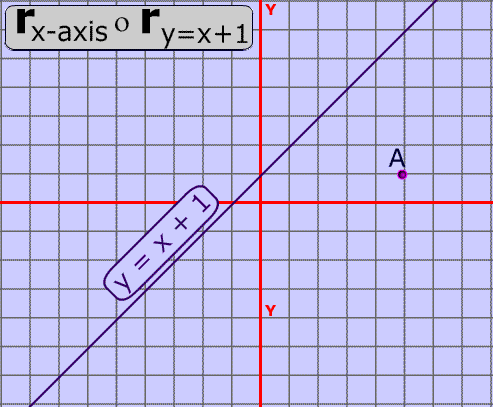
Solved 3 Reflection Across Y X 4 Reflectio 5 Chegg Com

How To Find A Reflection Image

Reflection Over A Line Expii

Reflection Over Y X And Y X Youtube

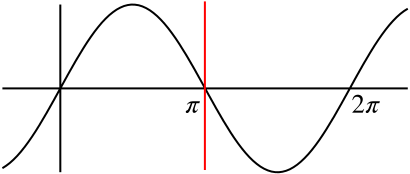
Solution What S The Result When We Reflect Y Sin X Twice Trigonometry Triangles To Functions Underground Mathematics

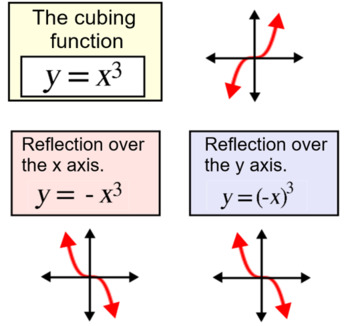
Reflections Of Functions Over The X Y Axes Intro 2 Assignments For Smart

10 Math Problems Transformation Reflection

Math Alive Geometry 1

Reflection Of A Point In A Line Msrblog

D Reflection Across Y X Brainly Com

Reflections Across A Line Other Than Axis Or Y X Power Jasmin Library Formative

Reflection Swiflearn

Solved Graph A Triangle Label It Lmn And Reflect It Over The Line Y X To Create Triangle L M N Describe The Transformation Using Words Draw Course Hero

Reflecting A Shape In Y X Using Cartesian Coordinates Key Stage 3

Learn About Reflection Over The Line Y X Caddell Prep Online

Inverse Function Reflection In Y Axis Mathematics Stack Exchange

What Are The Coordinates Of Point A 4 1 After It Has Been Reflected Over The Y Axis Socratic

How To Find A Reflection Image

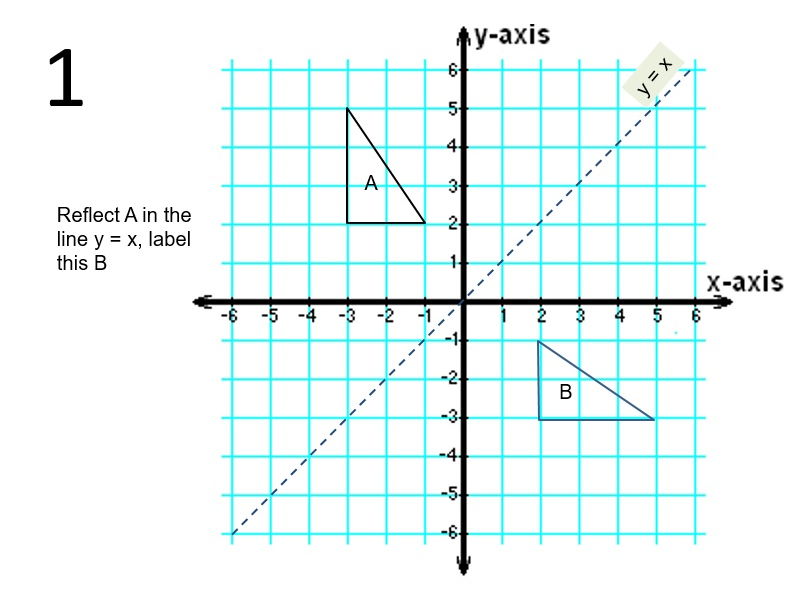
Diagonal Reflections In The Line Y X Teaching Resources

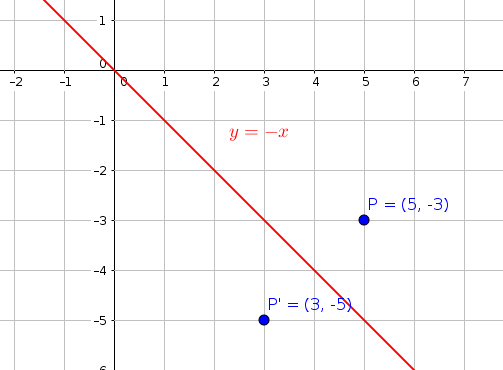
What Is The Reflection Image Of 5 3 In The Line Y X Socratic

Reflections Through The Axes And The Lines Y X And Y X Geogebra

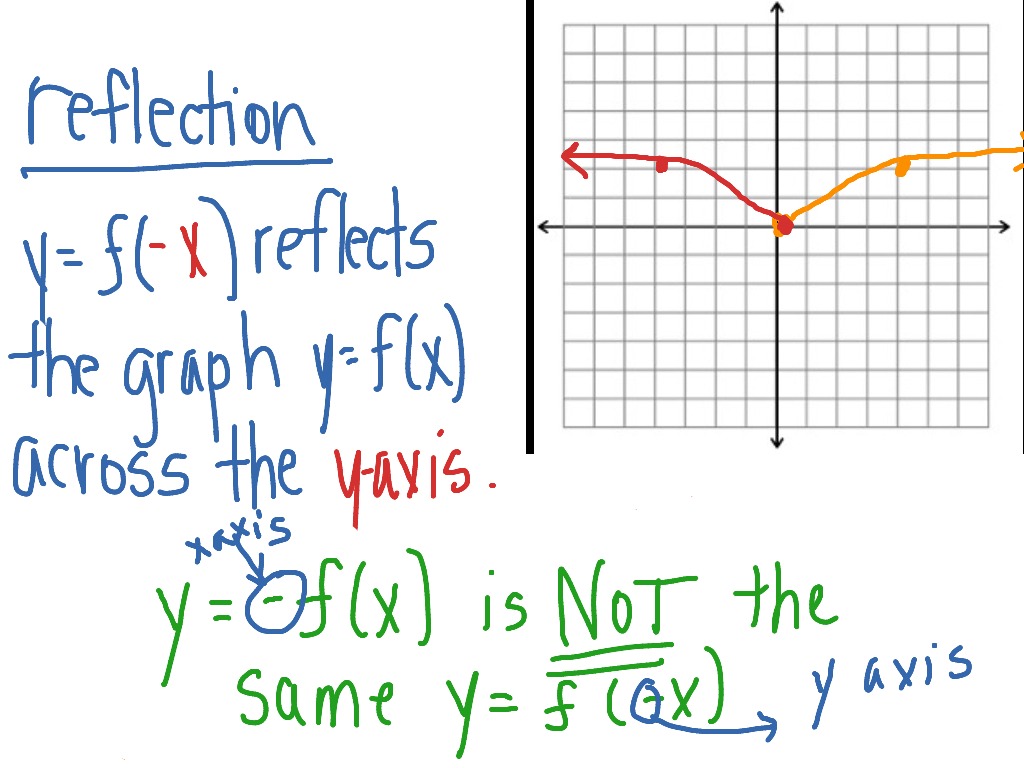
Reflection Across The Y Axis Math Functions Showme

Reflection Over The Line Y X Youtube

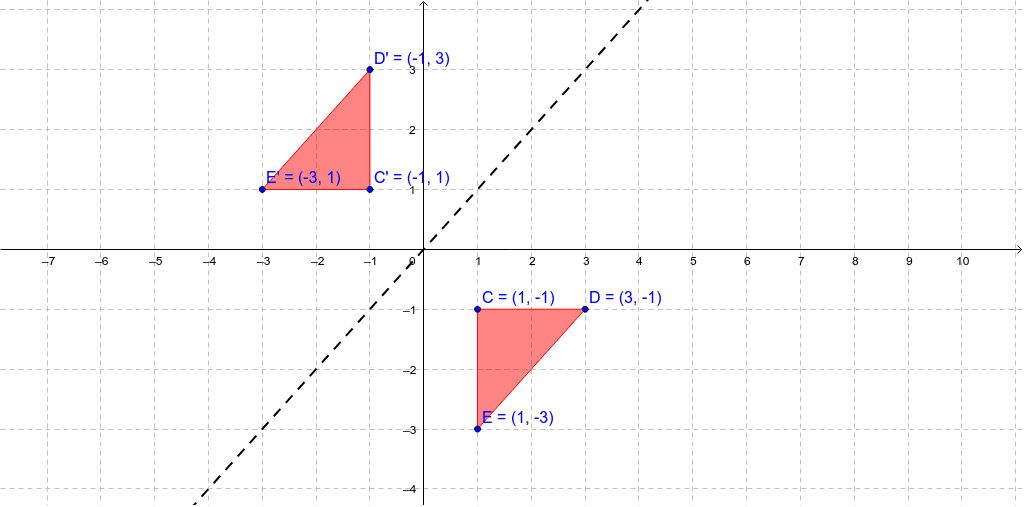
Reflection In The Line Y X Geogebra

Reflection Objectives D Gradereflect Shapes In Lines Such As X 2 Or Y 1 Describe Reflections Fully Identify Reflection Symmetry In 3 D Solids Prior Ppt Download

Reflections Of Trig Graphs Examsolutions

1

Reflection Over Y X Geogebra

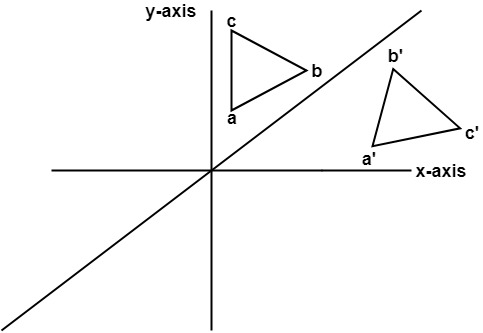
Which Graph Shows A Reflection Across The Line Y X Brainly Com

Solved Translations Multiple Choice Question A Reflection Over The Line Y X B Reflection Over The X Axis C Reflection Over The Y Axis D Transla Course Hero

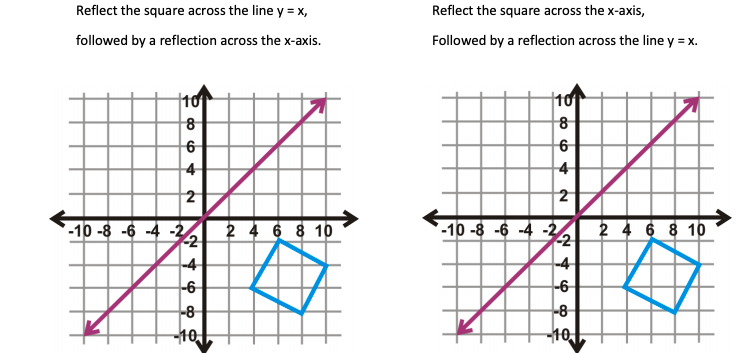
Solved Reflect The Square Across The Line Y X Followed By Chegg Com

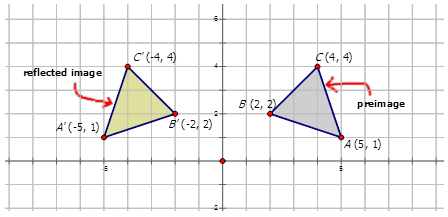
Rules For Reflections Read Geometry Ck 12 Foundation

Reflection Over Y X Geogebra

Reflection In The Line Y X Geogebra

How To Perform Reflections On A Coordinate Plane Geometry Study Com

Incoming Term: y x reflection, y x reflection line, y x reflection graph, y x reflection rule, y x reflection matrix, y x reflection equation, y x reflection formula, y x reflection geometry, y x reflection calculator, y x reflection rules 6, y x reflection formula 12,